FormDiagram
This tutorial provides a quick tour of the generation of FormDiagram from the parent package compas_tna.
The FormDiagram class can be created through purelly geometrical methods, such as:
from_lines: create the form diagram from lines provided by the user.from_mesh: create the form diagram from meshes provided by the user, enabling the combination with different meshing strategies, or to draw the diagram freely.
Also, a library of parametric diagrams is based on common layouts which will be described herein.
Diagrams Library
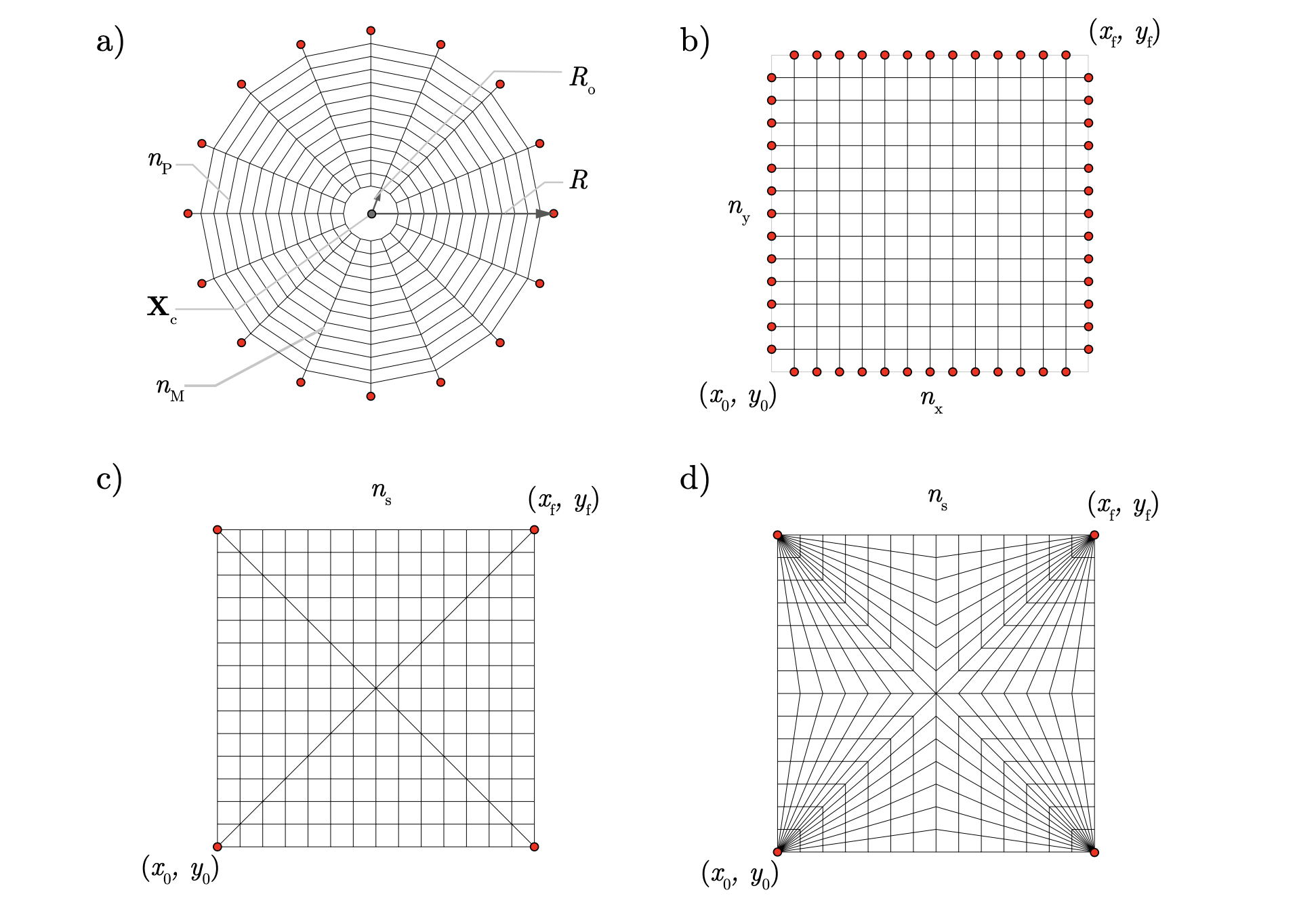
The figure above lists four parametric diagrams that can be created with the FormDiagram class based on parameters.
radial diagram: polar diagram defined by two discretisation parameters being the number of parallels or radial members \(n_\mathrm{P}\) and the number of circular hoops \(n_\mathrm{H}\). The location is defined by the central point position \(\mathbf{X}_\mathrm{c}\) and the size by the radius \(R\). Oculus openings can be considered with the parameter \(R_\mathrm{o}\). This diagram can be used to analyse problems on domes. The code to generate this diagram is below:
Long form:
from compas_tna.diagrams import FormDiagram
formdiagram = FormDiagram.create_circular_radial(center=(5.0, 5.0),
radius=5.0,
n_hoops=12,
n_parallels=16,
r_oculus=0.75)
Options are also provided to automatically add diagonals to the diagram with different options controlled by the parameter diagonal_type. This parameter, controls how diagonals are placed in the quads Options are [“split”, “straight”, “right”, “left”]. Default is “split”, when the X diagonals will be split at their intersection. If “straight”, both quad diagonals are added as straight lines. If “right”, the diagonals will point to the right (x positive) of the diagram. If “left”, the diagonals will point to the left (x negative) of the diagram.
orthogonal diagram: the orthogonal diagram is defined through two discretisation parameters \(n_\mathrm{x}, n_\mathrm{y}\), and the start and end dimensions in x and y directions \(x_\mathrm{span} = (x_\mathrm{0}, x_\mathrm{f})\) and \(y_\mathrm{span} = (y_\mathrm{0}, y_\mathrm{f})\). This diagram is suitable for performing analysis of continuously supported vaults, such as pavillion vaults. The square orthogonal diagram is presented in the Figure above can be generated by the following code:
from compas_tna.diagrams import FormDiagram
form = FormDiagram.create_ortho(x_span=(0.0, 10.0),
y_span=(0.0, 10.0),
nx=14,
ny=14,
fix='all')
cross diagram: the cross diagram corresponds to the orthogonal diagram added with the main diagonals, defined through identical parameters as in the orthogonal case. This diagram is used in the cross vault example. The cross diagram with \(n_\mathrm{s}=14\) can be constructed with:
from compas_tna.diagrams import FormDiagram
form = FormDiagram.create_cross(x_span=(0.0, 10.0),
y_span=(0.0, 10.0),
n=14)
fan diagram: unlike the orthogonal arrangement, the parallel segments arriving at the diagonals are directed to the corners. The fan receives two discretisation parameters \(n_\mathrm{f}\) and \(n_\mathrm{h}\) representing the number of fans and the number of hoops respectively. The span parameters are identical to the ones necessary to construct the cross diagram. This diagram is used in the alternative cross vault example.
from compas_tna.diagrams import FormDiagram
form = FormDiagram.create_fan(x_span=(0.0, 10.0),
y_span=(0.0, 10.0),
n_fans=14,
n_hoops=14)
To further explore the library of parametric diagrams, check the FormDiagram full documentation.