Mesh Supported by a Simple Arch

Summary

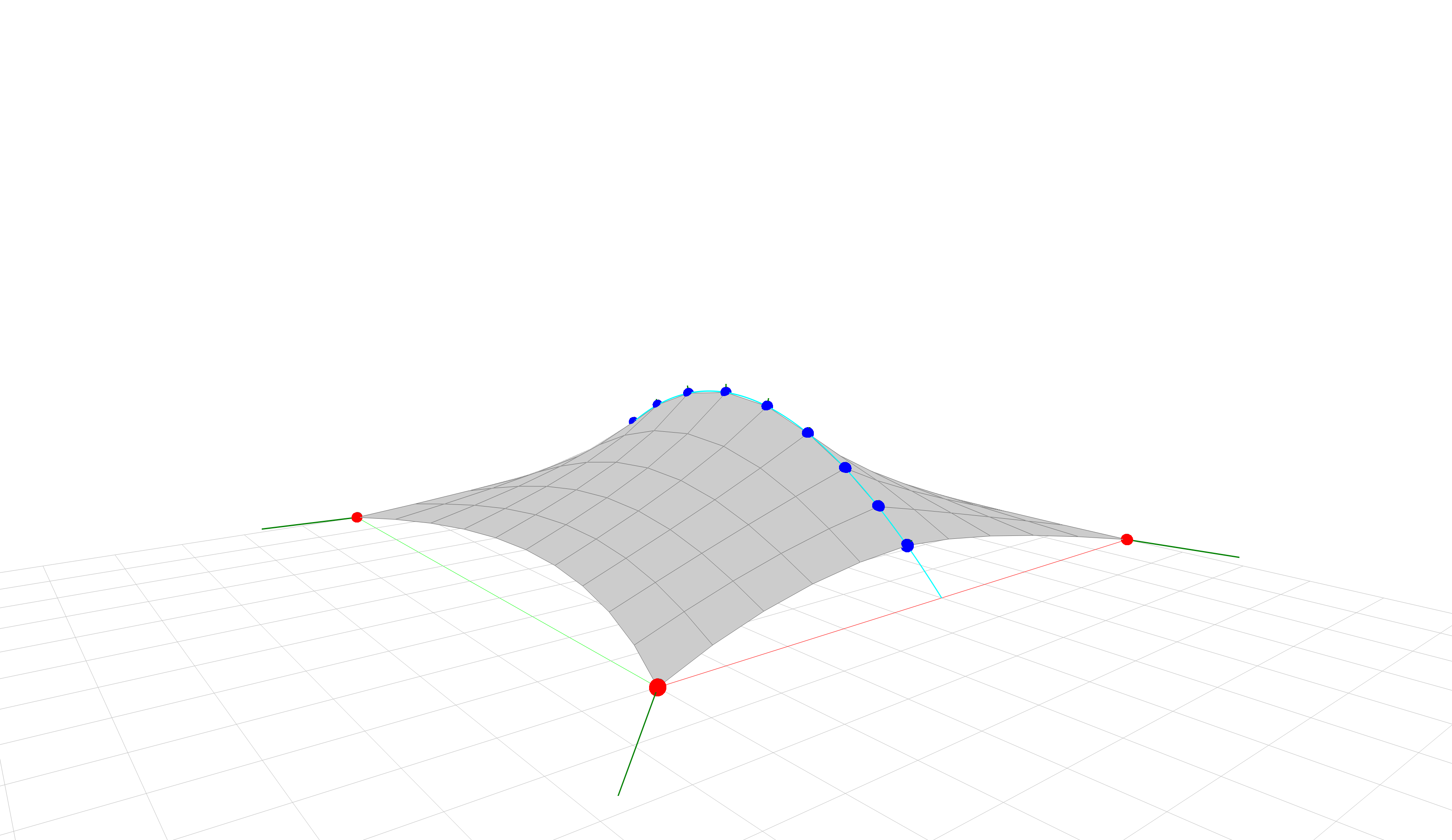
In this example, we construct a mesh from a meshgrid, fix the corner vertices, and constrain the middle vertices to a simple nurbs arch.

The contrained vertices slide along the arch under influence of the tangential component of their residual forces, until an equilibrium configuration is contained.

In the equilibrium configuration, the tangential compnents at the contrained vertices have vanished, leaving only the components normal to the constraint curve.

Code

from compas.colors import Color
from compas.datastructures import Mesh
from compas.geometry import Line
from compas.geometry import NurbsCurve
from compas.geometry import Point
from compas.geometry import Sphere
from compas.geometry import Vector
from compas_fd.constraints import Constraint
from compas_fd.solvers import fd_constrained_numpy
from compas_viewer import Viewer

# mesh

mesh = Mesh.from_meshgrid(dx=10, nx=10)

# vertices, edges

vertices = mesh.vertices_attributes("xyz")
edges = list(mesh.edges())

# fixed vertices

fixed = list(mesh.vertices_where(vertex_degree=2))

# loads

loads = [[0, 0, 0] for _ in range(mesh.number_of_vertices())]

# force densities

q = []
for edge in edges:
    if mesh.is_edge_on_boundary(edge):
        q.append(10)
    else:
        q.append(1.0)

# constraints

arch = NurbsCurve.from_points([[5, 0, 0], [5, 5, 5], [5, 10, 0]])
constraint = Constraint(arch)

constraints = [None] * mesh.number_of_vertices()
for vertex in mesh.vertices_where(x=5):
    constraints[vertex] = constraint
    fixed.append(vertex)

# =============================================================================
# Solve and Update
# =============================================================================

result = fd_constrained_numpy(
    vertices=vertices,
    fixed=fixed,
    edges=edges,
    forcedensities=q,
    loads=loads,
    constraints=constraints,
)

for vertex, attr in mesh.vertices(data=True):
    attr["x"] = result.vertices[vertex, 0]
    attr["y"] = result.vertices[vertex, 1]
    attr["z"] = result.vertices[vertex, 2]

# =============================================================================
# Visualization
# =============================================================================

viewer = Viewer()
viewer.renderer.camera.target = [5, 5, 0]
viewer.renderer.camera.position = [-3, -10, 10]

viewer.scene.add(mesh, show_points=False)

for vertex in mesh.vertices():
    point = Point(*mesh.vertex_coordinates(vertex))
    residual = Vector(*result.residuals[vertex])

    if vertex in fixed:
        ball = Sphere(radius=0.05, point=point)

        if constraints[vertex]:
            viewer.scene.add(ball.to_brep(), surfacecolor=Color.blue(), show_points=False)
        else:
            viewer.scene.add(ball.to_brep(), surfacecolor=Color.red(), show_points=False)

        viewer.scene.add(
            Line(point, point - residual * 0.1),
            linecolor=Color.green().darkened(50),
            lineswidth=3,
            show_points=False,
        )

viewer.scene.add(arch.to_polyline(), linecolor=Color.cyan(), lineswidth=3, show_points=False)

viewer.show()